Los investigadores de la Universidad Nacional de Singapur (NUS) han logrado un progreso emocionante en el campo de la metrología cuántica. La metrología cuántica utiliza efectos cuánticos para lograr mediciones de alta precisión sin precedentes. Su nuevo protocolo desarrollado tiene el potencial de beneficiar a tecnologías emergentes como la navegación y la detección de señales extremadamente débiles.

La metrología cuántica aprovecha las propiedades únicas de los sistemas cuánticos para lograr una sensibilidad mucho mayor que el límite clásico. Para superar el llamado límite cuántico estándar (SQL) y alcanzar el límite de Heisenberg definitivo (HL), generalmente se necesitan estados cuánticos altamente entrelazados, como el estado de Greenberger-Horne-Zeilinger (GHZ). Sin embargo, la generación, mantenimiento y medición de estos estados son extremadamente desafiantes, ya que son muy susceptibles a ruido ambiental y errores de lectura, lo que representa el principal obstáculo para aplicaciones prácticas.

Bajo el liderazgo del profesor Gong Jiangbin del Departamento de Física de la Facultad de Ciencias de la NUS, el equipo de investigación desarrolló una estrategia novedosa que elimina estos obstáculos. Su método aprovecha la dinámica de resonancia cuántica en sistemas de espín impulsados periódicamente, un modelo ampliamente estudiado conocido como trompo cuántico pateado.

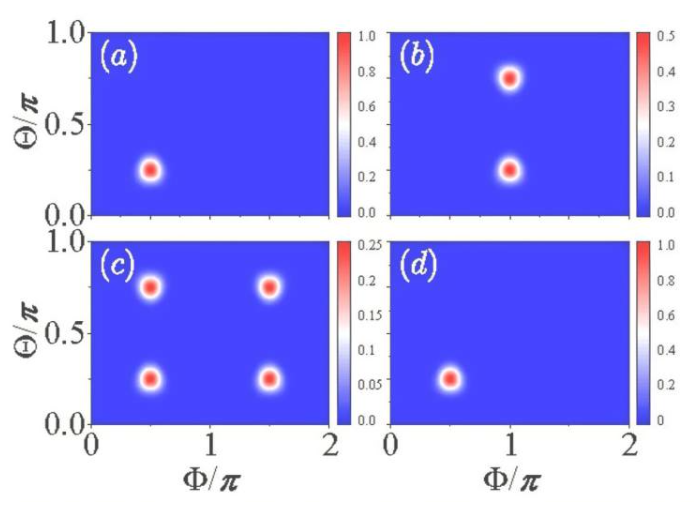
Su protocolo no comienza con estados altamente entrelazados frágiles, sino con un estado coherente de espín SU(2) robusto y fácil de preparar. A través de interacciones periódicas diseñadas con precisión, este estado inicial simple evoluciona naturalmente hacia un estado altamente entrelazado que codifica información cuántica. Bajo condiciones de resonancia especiales, el sistema regresa a su estado coherente original debido a la recursión cuántica, logrando una preparación simple y una lectura robusta.

Los resultados de la investigación se publicaron en la revista Physical Review Letters el 11 de junio de 2025.

El profesor Gong dijo: "Esta evolución de ida y vuelta significa que podemos comenzar y terminar en estados estables y amigables con los experimentos, mientras aún aprovechamos la sensibilidad cuántica mejorada generalmente asociada con estados entrelazados más desafiantes".

El equipo de investigación demostró que su protocolo alcanza la precisión de medición del límite de Heisenberg. La información de Fisher cuántica (QFI), que determina la precisión óptima alcanzable, crece con el cuadrado del número de partículas (espines) y el tiempo de sensado.

A diferencia de métodos anteriores, esta escala óptima se puede mantener durante períodos de tiempo más largos y es robusta incluso en presencia de ruido Markoviano (una forma común de decoherencia ambiental en sistemas cuánticos). Incluso bajo tal ruido, el protocolo mantiene una escala casi de Heisenberg con el número de espines, marcando un gran avance en la metrología cuántica práctica.

Una de las principales ventajas de este método es su viabilidad experimental. El protocolo se puede implementar utilizando hardware cuántico existente (incluyendo plataformas basadas en iones atrapados o átomos fríos), simplemente ajustando los parámetros operativos, sin necesidad de equipo especial o preparación de estados complejos.

"Este trabajo demuestra que las mediciones cuánticas ultraprecisas se pueden lograr sin superar las dificultades habituales. Al evitar la preparación de estados complejos y mejorar la resistencia al ruido, nuestro método abre nuevas posibilidades para el sensado cuántico práctico y escalable", añadió el profesor Gong.

Este progreso representa un avance conceptual en la metrología cuántica, proporcionando una vía experimental viable y resistente al ruido para lograr la precisión de medición del límite de Heisenberg. El protocolo aprovecha la dinámica de resonancia cuántica de estados iniciales simples, superando obstáculos de larga data en la preparación y lectura de estados, allanando el camino para aplicaciones prácticas de tecnologías de sensado cuántico de próxima generación.