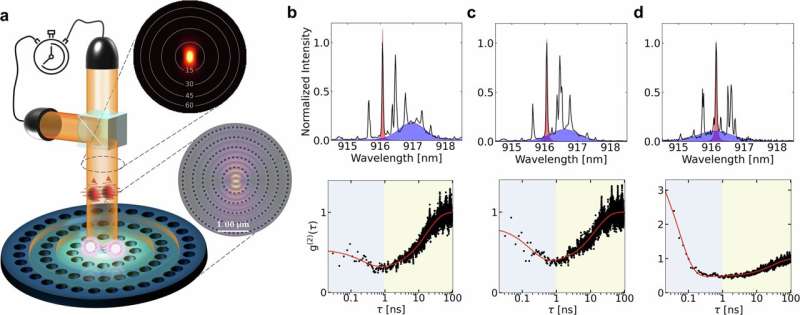
Aunque las computadoras cuánticas tienen el potencial de resolver problemas que desafían a las supercomputadoras, los qubits actuales son fácilmente interferidos por el entorno, acumulando errores rápidamente. La computación cuántica topológica se considera una esperanza para superar este problema, codificando la información cuántica en las propiedades geométricas de partículas exóticas para proteger la información. El profesor Aaron Lauda, de la Facultad de Letras y Ciencias Dornsife de la Universidad del Sur de California, señaló: "Los anyones de Ising son uno de los principales candidatos para construir computadoras cuánticas topológicas, pero por sí solos no pueden realizar todas las operaciones necesarias para una computadora cuántica universal."
El cómputo soportado por anyones de Ising depende de "trenzado", es decir, mover físicamente los anyones para ejecutar lógica cuántica. Sin embargo, este trenzado solo soporta operaciones limitadas, insuficientes para la computación cuántica universal. En un estudio publicado en Nature Communications, un equipo liderado por la Universidad del Sur de California demostró un nuevo método que, al introducir un nuevo tipo de anyón —el "anyón ignorado"—, hace que los anyones de Ising sean universales.
El nombre "anyón ignorado" refleja tanto su estatus previamente ignorado como la importancia de su nuevo descubrimiento. Este anyón emerge naturalmente de un marco matemático más amplio, proporcionando el elemento faltante en la caja de herramientas computacionales. El equipo de investigación utilizó la teoría cuántica de campos topológica no semi-simple, reteniendo objetos "de trazas cuánticas cero" descartados en modelos tradicionales, revelando la existencia de los "anyones ignorados". Cuando se combinan con anyones de Ising, solo mediante trenzado se puede lograr cómputo universal.
Ante los desafíos matemáticos introducidos por el marco no semi-simple, el equipo de Lauda diseñó una codificación cuántica que aísla las irregularidades matemáticas de la computación práctica. Lauda lo comparó con: "Diseñar una computadora cuántica en una casa con habitaciones inestables, asegurándonos de que todos los cálculos se realicen en áreas estructuralmente sólidas." Este avance indica que las matemáticas abstractas pueden resolver problemas de ingeniería concretos de maneras inesperadas, abriendo un nuevo capítulo en la ciencia de la información cuántica.
Esta investigación abre nuevas direcciones tanto en teoría como en práctica. El equipo está trabajando en expandir el marco a otros valores de parámetros y aclarar el rol de la unitariedad en TQFT no semi-simples. En el aspecto experimental, buscan identificar plataformas de materiales donde puedan aparecer "anyones ignorados" y desarrollar protocolos para convertir métodos de trenzado en operaciones cuánticas realizables.